Concepts
Drugs must get to their site of action to be useful, and in most cases, we administer drugs at sites other than the site of action. Understanding how drugs get to their site of action and how long they stay there is essential to making therapeutic decisions about which drug, what route, how much, how often, and for how long.
Classically, how drug moves through the body can be described with ADME, absorption, distribution, metabolism, and elimination. We will highlight the clinically important aspects of each stage of drug movement, as well as demonstrating the effect that differences in these parameters make in drug concentrations.
Remember that we most commonly measure the concentrations of drug in the plasma or serum, even though many of our target cells for drug activity are outside the plasma. This is based on the assumption that plasma concentrations correlate with tissue concentrations, so conclusions about tissue concentration can be made from plasma concentrations. This may not be true for all drugs, but it holds true for enough important compounds that it is a reasonable assumption until proven otherwise.
Simulated graphs are presented below to demonstrate the effects of changes in pharmacokinetic parameters. These simulations were performed, at the website of David Bourne.
Absorption
Absorption is usually defined as the proportion of drug moving from the administered drug product into the bloodstream. Drugs administered IV are assumed to be 100% absorbed by definition. For drugs administered PO, major losses of drug occur by not crossing enterocyte membranes in the GI tract, via metabolism in the gut wall (e.g., peptidases), and via metabolism in the liver (since drug absorbed from the GI tract enters portal circulation first and can therefore bring drug into contact with enzymes in hepatocytes before it enters peripheral circulation). Absorption rate can be indicated by the half-life of absorption, sometimes designated as t1/2α.
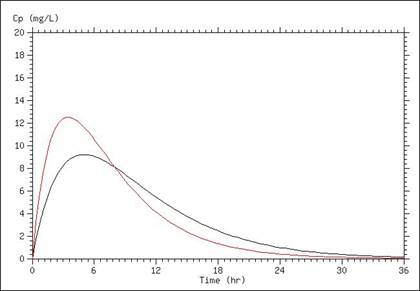
A simulation of serum concentrations is presented in the graph below, in which the only difference between the two lines is a doubling of the absorption rate. This results in a higher Cmax, as well as a shorter time above any given concentration (once absorption is mostly completed).
Distribution
Distribution refers to the movement of drug from the bloodstream into the interstitial fluid and into other tissues. The mathematical parameter usually used to describe distribution is the volume of distribution (V or Vd or VDss). The volume of distribution can be defined as the apparent volume of fluid needed to contain the total amount of a drug in the body at the same concentration as it is in the plasma. It is an indication of whether drug tends to remain in the vascular system, in total body water, or in tissues.
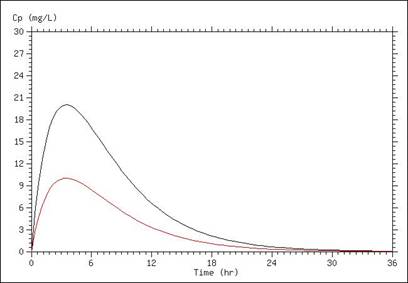
A simulation of serum concentration is shown below, in which the only difference between the two lines is a doubling of the volume of distribution. In this case, a higher volume of distribution results in a lower peak concentration and lower concentrations throughout the time course.
Metabolism
Metabolism may change pro-drug to active drug, active drug to active metabolite, or active drug to inactive metabolite. A basic understanding of how a drug is metabolized (or if a drug is metabolized) will aid in clinical decision-making in cases in which mechanisms of metabolism are compromised because of disease. Active metabolites should also be considered when examining drug concentration data, since graphs of concentration data may be misleading if they do not contain parent drug and active metabolite.
Elimination
Elimination generally refers to elimination from plasma or serum, and the rate of elimination is designated as ka. Elimination half-life is the time taken for the serum concentration to drop by half, and is often designated as t1/2β. For the most part, it is assumed that the drugs we use regularly for therapeutic purposes follow first order elimination. This means that a constant proportion of drug is removed from the body per unit time. There are some exceptions, in which a constant amount of drug is removed from the body per unit time, designated zero order. Zero order elimination generally occurs when clearance mechanisms have become saturated, so zero order kinetics are more often – Seen with toxic doses of drug.
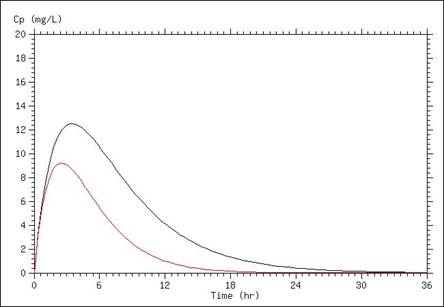
A simulation of serum concentrations in which the elimination rate is doubled is presented below. When elimination rate is increased, overall concentrations are lower as is the peak concentration.
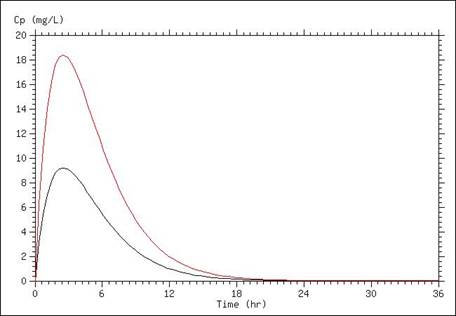
A simulation of serum concentrations is presented below, in which the only difference between the lines is a doubling of the dose administered. Careful examination of the graph reveals that the peak concentration in the curve representing the doubled dose is twice that of the lower dose, and the time that concentrations remain above a particular level are moved over one half-life (in this case half-life was set at 1.7 hours).
Mathematical Descriptions
To be complete, we should briefly discuss how pharmacokineticists generate mathematical descriptions of drug movement to allow for predictions and to explain drug behavior and clinical effects. The major methods of mathematical modeling of drug concentration data include compartmental and non-compartment modeling. Compartmental modeling is used to mathematically describe drug movement under particular assumptions about how drugs act; the compartments assumed are not anatomical compartments but rather are artificial methods to describe rates of drug movement. Non-compartmental modeling is based on statistical moment theory, which makes no assumption about how drugs move but rather assumes the drug concentrations at a given time point are independent and can therefore be modeled in a stochastic manner. Regardless of how modeling and mathematically descriptions are performed, the goal is to explain why drug is moving in a particular way and to make predictions about drug movement.
References
Brunton, LL, Lazo, JS, and Parker, KL, Goodman & Gilman’s The Pharmacological Basis of Therapeutics, 11th edition, McGraw-Hill, 2006